Law of total probability
In probability theory, the law (or formula) of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.
Contents |
Statement
The law of total probability is[1] the proposition that if 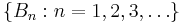 is a finite or countably infinite partition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event
is a finite or countably infinite partition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event 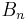 is measurable, then for any event
is measurable, then for any event  of the same probability space:
of the same probability space:
or, alternatively, [1]
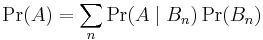 ,
,
where, for any 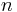 for which
for which 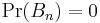 these terms are simply omitted from the summation, because
these terms are simply omitted from the summation, because 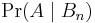 is finite.
is finite.
The summation can be interpreted as a weighted average, and consequently the marginal probability, 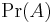 , is sometimes called "average probability";[2] "overall probability" is sometimes used in less formal writings.[3]
, is sometimes called "average probability";[2] "overall probability" is sometimes used in less formal writings.[3]
The law of total probability can also be stated for conditional probabilities. Taking the 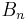 as above, and assuming
as above, and assuming  is not mutually exclusive with
is not mutually exclusive with  or any of the
or any of the 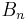 :
:
Applications
One common application of the law is where the events coincide with a discrete random variable X taking each value in its range, i.e. 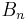 is the event
is the event  . It follows that the probability of an event A is equal to the expected value of the conditional probabilities of A given
. It follows that the probability of an event A is equal to the expected value of the conditional probabilities of A given  . That is,
. That is,
where Pr(A|X) is the conditional probability of A given X,[3] and where EX denotes the expectation with respect to the random variable X.
This result can be generalized to continuous random variables (via continuous conditional density), and the expression becomes
where 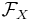 denotes the sigma-algebra generated by the random variable X.
denotes the sigma-algebra generated by the random variable X.
Other names
The term law of total probability is sometimes taken to mean the law of alternatives, which is a special case of the law of total probability applying to discrete random variables. One author even uses the terminology "continuous law of alternatives" in the continuous case.[4] This result is given by Grimmett and Welsh[5] as the partition theorem, a name that they also give to the related law of total expectation.
See also
References
- ^ a b Zwillinger, D., Kokoska, S. (2000) CRC Standard Probability and Statistics Tables and Formulae, CRC Press. ISBN 1-58488-059-7 page 31.
- ^ Paul E. Pfeiffer (1978). Concepts of probability theory. Courier Dover Publications. pp. 47–48. ISBN 9780486636771. http://books.google.com/books?id=_mayRBczVRwC&pg=PA47.
- ^ a b Deborah Rumsey (2006). Probability for dummies. For Dummies. p. 58. ISBN 9780471751410. http://books.google.com/books?id=Vj3NZ59ZcnoC&pg=PA58.
- ^ Kenneth Baclawski (2008). Introduction to probability with R. CRC Press. p. 179. ISBN 9781420065213. http://books.google.com/books?id=Kglc9g5IPf4C&pg=PA179.
- ^ Probability: An Introduction, by Geoffrey Grimmett and Dominic Welsh, Oxford Science Publications, 1986, Theorem 1B.
- Introduction to Probability and Statistics by William Mendenhall, Robert J. Beaver, Barbara M. Beaver, Thomson Brooks/Cole, 2005, page 159.
- Theory of Statistics, by Mark J. Schervish, Springer, 1995.
- Schaum's Outline of Theory and Problems of Beginning Finite Mathematics, by John J. Schiller, Seymour Lipschutz, and R. Alu Srinivasan, McGraw-Hill Professional, 2005, page 116.
- A First Course in Stochastic Models, by H. C. Tijms, John Wiley and Sons, 2003, pages 431–432.
- An Intermediate Course in Probability, by Alan Gut, Springer, 1995, pages 5–6.
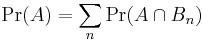
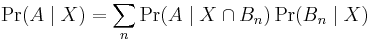
![\Pr(A)=\sum_n \Pr(A\mid X=x_n)\Pr(X=x_n) = \operatorname{E}_X[\Pr(A\mid X)] ,](/2012-wikipedia_en_all_nopic_01_2012/I/a1d1f51bfdb2120f5076f0d6e310b94f.png)
![\Pr(A)= \operatorname{E}[\Pr(A\mid \mathcal{F}_X)],](/2012-wikipedia_en_all_nopic_01_2012/I/e26c8d6d420a5421ac0de0200820f0aa.png)